- Problemstellung
- Physikalisches Modell
Problemstellung
Durch die Infiltration von nicht wasserlöslichen Stoffen in einen Grundwasserleiter entsteht ein Mehrphasenfließsystem. Diese Stoffe können Verunreinigungen wie z.B. Benzol, Teer, PAK und TCE (Tetrachlorethen) sein. Es handelt sich dabei um organische Stoffe, die kaum wasserlöslich (hydrophob) sind. Sie werden als NAPL (Non-Aqueous Phase Liquid) bezeichnet und haben eine höhere Dichte als Wasser (Dense NAPL) oder geringere Dichte als Wasser (Light NAPL). Daraus resultiert das vom Wasser abweichende Ausbreitungsverhalten als zusammenhängende Phase im Grundwasserleiter, das mit herkömmlichen Einphasen-Stofftransportmodellen physikalisch nicht beschrieben werden kann. Um Aussagen über die Verteilung und Ausbreitung solcher Stoffe im Boden sowie die Wirkung von Sanierungsverfahren treffen zu können, ist die Modellierung mit einem Mehrphasenströmungsmodell notwendig.

Treffen zwei Phasen im Porenraum aufeinander, treten an den Phasengrenzen Wechselwirkungen auf. Die wesentlichen Parameter sind Kapillarität und Permeabilität. Sie sind jeweils abhängig vom Sättigungsverhältnis der beiden Phasen Wasser und NAPL.
Physikalisches Modell
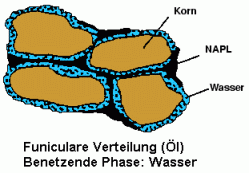
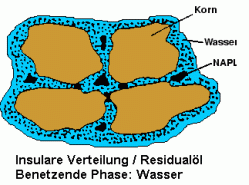
Der Unterschied zwischen benetzenden und nicht-benetzenden Fluiden resultiert aus der Größe des Randwinkels y. Das linke Bild zeigt die verschiedenen Benetzungseigenschaften des NAPLs und des Wassers gegenüber der Bodenmatrix. das Wasser wird hierbei als benetzend, das NAPL als nicht-benetzend bezeichnet, weil das Wasser gegenüber dem NAPL die geringere Grenzflächenspannung aufweist.
Ebenfalls gilt, dass mit abnehmendem Krümmungsradius der Kapillardruck steigt und dass das benetzende Fluid in die kleinen Poren gedrängt wird. Andererseits wird mit größer werdenden Krümmungsradien der Kapillardruck kleiner und das nicht benetzende Fluid besetzt den Porenraum. Die rechte Abbildung zeigt die vom Krümmungsradius abhängige Verteilung von benetzendem und nicht-benetzendem Fluid im Porenraum.
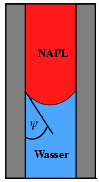
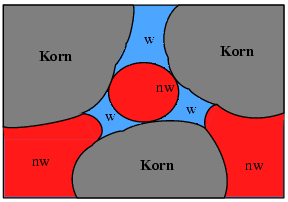
Die Kapillarität ist eine bestimmte Einflußgrösse bei der Bewegung der zwei Phasen im Porenraum. Jedes der Fluide übt einen konkreten Druck auf die Grenzfläche aus. Die Differenz zwischen den beiden Fluidspannungen bewirkt eine Grenzflächenspannung, die über den gesamten Meniskus wirkt und als Kapillardruck bezeichnet wird.
In der Abbildung wird deutlich, dass bei einem durchlässigen Medium (I) für eine gegebene Sättigung der Kapillardruck gegenüber einem schwach durchlässigen Medium (II) klein ist. Die Phasen im Porenraum behindern sich gegenseitig in ihrer Bewegung. Diesem Phänomen wird durch die relative Permeabilität Rechnung getragen, die abhängig von der Sättigung Werte zwischen 0 und 1 annehmen kann.

Mathematisches Modell
Das Strömungsverhalten beweglicher Fluide im Porengrundwasserleiter läßt sich durch kontinuumsmechanische Bewegungsgleichungen mathematisch beschreiben. Diese Bewegungsgleichungen werden auf der Grundlage des Gesetzes von Darcy über ein repräsentatives Einheitsvolumen aufgestellt.
Bei dem hier gewählten Ansatz sind der Druck und die Sättigung der benetzenden Phase (z.B. Wasser) die zu berechnenden primären Unbekannten.
Für die nicht-benetzende Phase (nw = non-wetting):

Für die benetzende Phase:

Diese zu lösenden Differentialgleichungen sind durch die nichtlinearen Abhängigkeiten des Kapillardrucks und der relativen Permeabilität von der Sättigung der benetzenden Phase miteinander gekoppelt. Durch die Vorgabe von Rand- und Anfangsbedingungen ist das zeitabhängige Differentialgleichungssystem lösbar.

Numerisches Modell
Methode der Finiten Elemente im Ort 2D-isoparametrische bilineare Ansatzfunktion

Finite Differenzen-Ansatz in der Zeit:

Zeitschrittweitensteuerung
Linearisierung durch ein gedämpftes Newtonverfahren
Lösung der Gleichungssystem durch Super LU
Berücksichtigung von Heterogenitäten

Anwendung
In einem Laborexperiment wurde ein Behälter mit den Abmessungen 70 x 50 x 6 cm mit Sanden verschiedener Durchlässigkeiten gefüllt. Im Anfangszustand vor Beginn des Experiments ist der Sand vollständig mit Wasser gesättigt. Der Behälter ist nur an den seitlichen Rändern offen. Am oberen Rand befindet sich eine Öffnung zum Infiltrieren des DNAPLs.
Das Experiment beginnt, wenn das TCE eingeleitet wird. Das Fluid ist schwerer als Wasser und fließt aufgrund der Gravitation nach unten, poolt auf der ersten weniger durchlässigen Linse (Sand3) auf, bringt jedoch den erforderlichen Verdrängungsdruck nicht auf und umströmt die Linse. In einiger Zeit wird der Kapillardruck größer als der Verdrängungsdruck und das NAPL infiltriert in die Linse. Das Wasser wird verdrängt und strömt an den Seiten aus.


| Dichte [kg/m³] | Blog | |
|---|---|---|
| Spalte 1 | ist linksbündig | € 150 |
| Spalte 2 | ist zentriert | € 44 |
| Spalte 3 | ist rechtsbündig | € 3 |

