- Einleitung
- Modell und Parameter
- Theoretischer Hintergrund
- Diskretisierung
- Vergleich der Berechnungsergebnisse
- Literatur
Einleitung
Die Verifizierung erfolgt für eine 1D stationäre Strömung und einen 1D Transport. Der Schadstoffeintrag erfolgt permanent und konstant. Der Ort des Eintrags ist am Modellrand, was eine sehr starke Einschränkung im Vergleich zu realen Verhältnissen darstellt. Der Grundwasserleiter ist homogen, isotrop, gespannt und besitzt theoretisch eine unendliche Ausdehnung mit einer konstanten Mächtigkeit und horizontalen Piezometerhöhen. Gesucht ist die Art und Weise der Schadstoffausbreitung über die Zeit. Für dieses Problem finden sich in der Literatur analytische Lösungsansätze.
Modell und Parameter
Die Länge des Modells beträgt L = 25 0m und eine Breite von B = 50 m. Das Beispielmodellgebiet soll des Weiteren folgende Eigenschaften aufweisen:
Durchlässigkeitsbeiwert: kf = 5*10-4 m/s (KWER)
Mächtigkeit: m = 16 m (MAEC)
Porosität: n e= 0,2 (PORO)
Dispersivität αL = 5 m (DISP)
Anfangspotentiale: Hl = 25,00 m Hr = 15,00 m(POTE)
Schadstoffkonzentration: c0 = 150 mg/m3 (1KON)
Verzögerungsfaktor: R = 1
Abbaukonstante: λ = 0
Theoretischer Hintergrund
Die analytische Transportgleichung für einen 1D Transport lautet:

Darin bedeutet:
• c: Konzentration [mg/m3]
• t: Zeit [s]
• u: Abstandsgeschwindigkeit [m/s]
• R: Verzögerungsfaktor [-]
• DL: longitudinale Dispersionskoeffizient [m2/s]
• λ: Abbaukonstante [1/s]
Der Verzögerungsfaktor berechnet sich mit:

und der longitudinale Dispersionskoeffizient zu:

.
Die Anfangsbedingung lautet:

und die Randbedingungen sind gegeben mit:

und

Dies führt zur Basislösung der Transportgleichung:

Darin bedeutet:
• ΔM: gesamte Stoffmasse [mg]
• ne: effektive Porosität [-]
• ca: Konzentration der adsorbierten Phase [mg/m3]
• ρ: Dichte des trockenen Matrixmaterials [t/m3]
• B: Streifenbreite [m]
• m: Mächtigkeit des Grundwasserleiters [m]
• αL: Dispersivität [m]
ΔM berechnet sich mit

Die Lösung für einen eindimensionalen Transport in homogener Parallelströmung bei einem permanenten und konstanten Stoffeintrag am Modellrand x = 0 und dem Start des Eintrags im Zeitpunkt t = 0 ergibt sich dann zu:

In dieser Gleichung bedeutet neben den schon genannten Bezeichnungen:
•

: Zugaberate des Stoffeintrags [mg/s]
• γ: Aktivitätskoeffizient [-]
• c0: Anfangsverteilung der Stoffkonzentration [mg/m3]
In dieser Gleichung berechnet sich c0 und γ mit:


Diskretisierung
In der transport_1D.zip Datei befindet sich die Datei Transport_1D.net. Mit dieser Netzdatei ist die Verifizierung durchgeführt worden. Es wurde ein Horizontalmodell mit der Zeiteinheit Jahr erstellt. Die Eingabeparameter stehen in der Tabelle im Abschnitt "Modell und Parameter". Die Berechnung ist für Zeiten von 2, 5, 8 und 10 Tagen erfolgt. Das verwendete Netz ist in der folgenden Abbildung dargestellt.


Vergleich der Berechnungsergebnisse
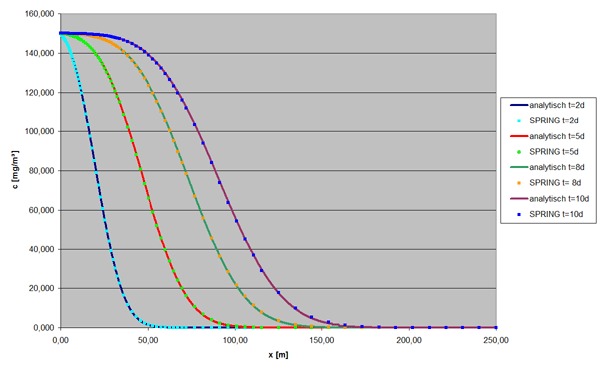
In der folgenden Abbildung sind die Ergebnisse von SPRING und der analytischen Lösung gegenüber gestellt. Die analytische Lösung ist mit der Datei Transport_1D.xls berechnet worden. Diese befindet sich ebenfalls in der transport_1D.zip Datei. Es ist deutlich zu sehen, dass die Lösung von SPRING kaum abweicht. [Anmerkung: In Excel 2000 muss für die Formeln erfc eingegeben werden. In EXCEL 2002 heißt die Funktion statt erfc jetzt Gausfkompl. Die Berechnung von z.B. erfc(-0,5) erfolgt etwas umständlicher, da EXCEL an dieser Stelle falsch rechnet.]
Literatur
[David] Ioan David; Grundwasserhydraulik Strömungs- und Transportvorgänge, Vieweg, 1997
[Kinzelbach] W. Kinzelbach; Numerische Methoden zur Modellierung des Transports von Schadstoffen im Grundwasser, Oldenbourg, 1987
[SPRING] SPRING; Simulation of Processes in Groundwater, Programm- beschreibung,Version 3.2

