- Einleitung
- Modell und Parameter
- Theoretischer Hintergrund
- Diskretisierung
- Vergleich der Berechnungsergebnisse
- Literatur
Einleitung
Dieses Berechnungsbeispiel betrachtet einen homogenen, isotropen und gespannten Grundwasserleiter aus dem bei einer stationä Strömung aus einem Brunnen Wasser entnommen wird. Gesucht ist die sich einstellende Absenkung des Grundwasserspiegels auf Grund der Entnahme. Für dieses Problem finden sich in der Literatur analytische Lösungsansätze.
Modell und Parameter
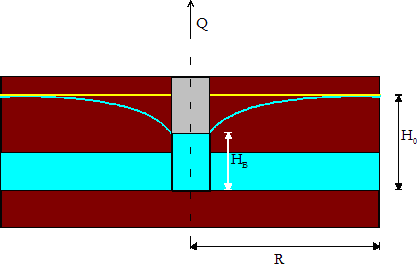
In der unten stehenden Abbildung ist eine prinzipielle Darstellung der Grundwasserabsenkung eines gespannten Grundwasserleiters mit der Entnahme mittels eines Einzelbrunnens dargestellt.
Das Beispielmodellgebiet soll folgende Eigenschaften aufweisen:
Durchlässigkeitsbeiwert: \(k_f = 5\cdot 10^{-4}\,\tfrac{\text{m}}{\text{s}}\) (KWER)
Mächtigkeit: \(m = 10\,\text{m}\) (MAEC)
Geländeangaben: \(\text{Oberkannte} = 45\,\text{m}\), \(\text{Unterkannte} = 0.01\,\text{m}\)
Reichweite: \(R = 500\,\text{m}\) (Modellausdehnung)
Brunnenradius: \(r_0 = 0.3\,\text{m}\)
Anfangspotential: \(H_0 = 40.00\,\text{m}\) (POTE)
Entnahmemenge: \(Q = -600\,000\,\tfrac{\text{m}^3}{\text{s}}\) (KNOT)
Theoretischer Hintergrund
Für die analytische Lösung einer 2-D Strömung wird mit der Potentialfunktion und der Stromfunktion eine Laplace partielle Differentialgleichung hergeleitet. Die differenzierbare Funktion einer komplexen Variablen für dieses Problem lautet:
\(F(z) = -\frac{Q}{2\pi} \cdot \ln(z) = -\frac{Q}{2\pi} \cdot \ln\left(x + i \cdot y\right)\)
Mit der Potential- und Stromfunktion
\(\varphi(x,y) = \text{Re}\left\{F(z)\right\} = -\frac{Q}{2\pi} \cdot \ln\left(\sqrt{x^2 + y^2}\right) = -\frac{Q}{2\pi} \cdot \ln(r)\)
\(\psi(x,y) = \text{Im}\left\{F(z)\right\} = -\frac{Q}{2\pi} \cdot \arctan\left(\frac{y}{x}\right)\)
ergeben sich kreisförmige Potentiallinien und geradlinige Stromlinien. Mit den Randbedingungen \(h(R) = H_0\) und \(h(r_0) = H_B\) können die Ergiebigkeit und die Piezometerhöhen bestimmt werden. Die Ergiebigkeit des Brunnen ermittelt sich mit den gegebenen Randbedingungen über
\(-\frac{Q}{2\pi} \ln(r) = \varphi(x,y) = -k_f \cdot m \cdot h + c\)
zu
\(Q = \frac{2\pi \cdot k_f \cdot m \cdot \left(H_0 - H_B\right)}{\ln\left(\frac{R}{r_0}\right)}\text.\)
Die Standrohrspiegelhöhe lässt sich bestimmen mittels
\(h(r) = H_B + \frac{Q}{2\pi \cdot k_f \cdot m} \cdot \ln\left(\frac{R}{r_0}\right)\text.\)
Dies ist die von Thiem hergeleitete Brunnenformel für stationäre Strömungsverhältnisse. Wenn die Entnahme vorgegeben ist und die sich einstellende Höhe im Brunnen berechnet werden soll, geschieht dies mit der Umstellung der Funktion
\(Q = \frac{2\pi \cdot k_f \cdot m \cdot \left(H_0 - H_B\right)}{\ln\left(\frac{R}{r_0}\right)}\)
zu
\(H_B = H_0 - \frac{Q\cdot \ln\left(\frac{R}{r_0}\right)}{2\pi \cdot k_f \cdot m}\text.\)
Mit den Angaben aus dem Abschnitt "Modell und Parameter" bezüglich der Eigenschaften des Grundwasserleiters ergibt sich die Höhe am Rand des Brunnens zu
\(H_B = H_0 - \frac{Q \cdot \ln\left(\frac{R}{r_0}\right)}{2\pi \cdot k_f \cdot m} = 40 - \frac{0.019 \cdot \ln\left(\frac{500}{0.3}\right)}{2\cdot\pi \cdot 0.0005 \cdot 10} = 35.51\,\text{m}\text.\)
Diskretisierung
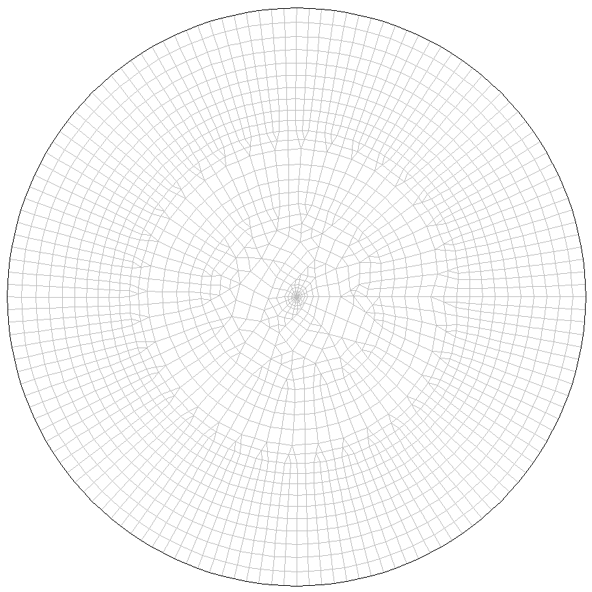
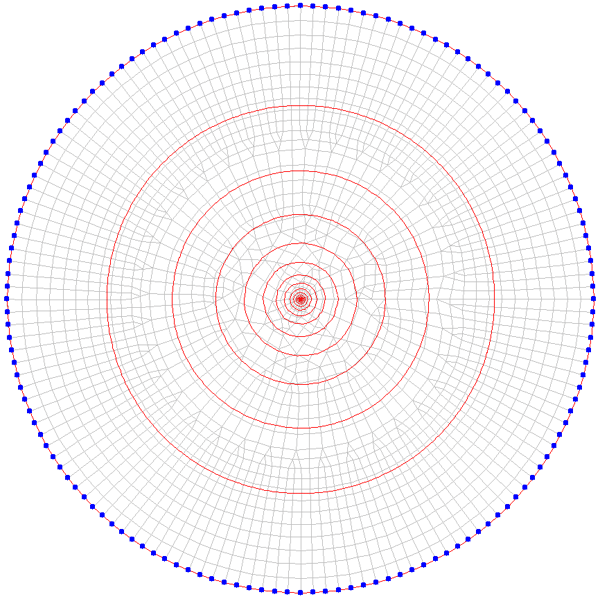
In der Brunnen_ge_s.zip Datei befindet sich die Datei Brunnen_gesp_stat.net. Mit dieser Netzdatei ist die Verifizierung durchgeführt worden. Es wurde ein Horizontalmodell mit der Zeiteinheit Jahr erstellt. Die Eingabeparameter stehen in der Tabelle im Abschnitt "Modell und Parameter". Das verwendete Netz ist in der folgenden Abbildung dargestellt.
Vergleich der Berechnungsergebnisse
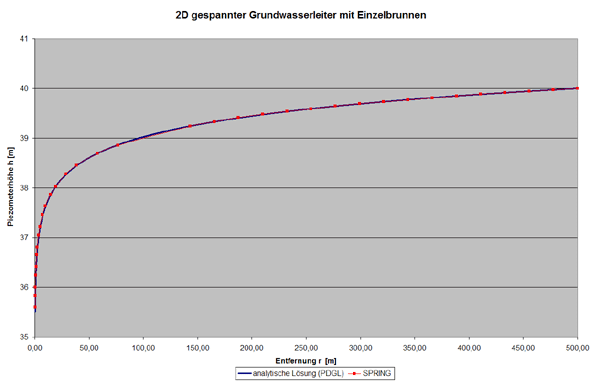
In der folgenden Abbildung sind die Ergebnisse von SPRING und der analytischen Lösung gegenüber gestellt. Die analytische Lösung ist mit der Datei Brunnen_gesp_stat.xls berechnet worden. Diese befindet sich ebenfalls in der brunnen_ge_s.zip Datei. Es ist deutlich zu sehen, dass die Lösung von SPRING kaum abweicht. Der maximale Unterschied zwischen den zwei berechneten Potentialhöhen betrÄgt 0,09 m. Durch eine weitere Verfeinerung des Netzes in der Nähe des Entnahmepunktes, ist zu erwarten, dass diese Differenz noch kleiner wird.
Literatur
[David] Ioan David; Grundwasserhydraulik Strömungs- und Transportvorgänge, Vieweg, 1997
[Kinzelbach] W. Kinzelbach; Numerische Methoden zur Modellierung des Transports von Schadstoffen im Grundwasser, Oldenbourg, 1987
[Kinzelbach] W. Kinzelbach und Rausch, R., Grundwassermodellierung Eine Einführung mit Übungen, Gebrüder Bornträger, 1995
[SPRING] SPRING; Simulation of Processes in Groundwater, Programm- beschreibung,Version 3.2