- Einleitung
- Modell und Parameter
- Theoretischer Hintergrund
- Diskretisierung
- Vergleich der Berechnungsergebnisse
- Literatur
Einleitung
Dieses Berechnungsbeispiel betrachtet einen homogenen, isotropen und gespannten Grundwasserleiter aus dem bei einer instationären Strömung aus einem Brunnen Wasser entnommen wird. Gesucht ist die sich einstellende Absenkung des Grundwasserspiegels auf Grund der Entnahme. Für dieses Problem findet sich in der Literatur der analytische Lösungsansatze nach Theis.
Modell und Parameter
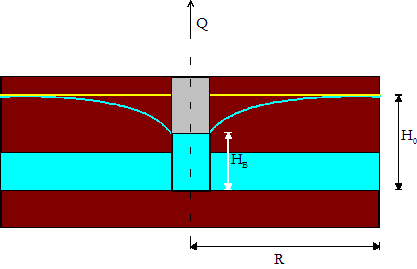
In der unten stehenden Abbildung ist eine prinzipielle Darstellung der Grundwasserabsenkung eines gespannten Grundwasserleiters mit der Entnahme mittels eines Einzelbrunnens dargestellt.
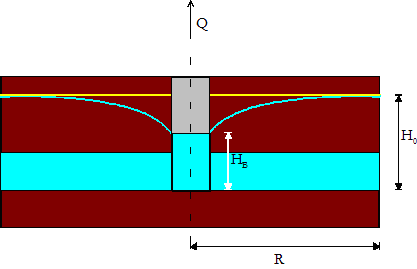
Das Beispielmodellgebiet soll folgende Eigenschaften aufweisen:
Durchlässigkeitsbeiwert: kf = 5*10-4 m/s (KWER)
Mächtigkeit: m = 10 m (MAEC)
Geländeangaben: Oberkannte = 45 m, Unterkante = 0,01m (GELA, UNTE)
Reichweite: R = 725 m (Modellausdehnung)
Brunnenradius: r0 = 0,3 m
Anfangspotential: H0 = 40,00 m (POTE, EICH)
Entnahmemenge: Q = -600000 m3/s (KNOT)
Speicherkoeffizient: S = 0,2 (SPEI)
Der betrachtete Zeitraum sind 100 Tage. Die Berechnung erfolgt für 200 Zeitschritte mit einer Zeitschrittweite von 0,5 Tagen.
Theoretischer Hintergrund
Die analytische Lösung von Theis ermöglicht die Berechnung für instationäre Strömungsverhältnisse. Die Herleitung beruht auf folgenden Vorraussetzungen. Der Grundwasserleiter muss gespannt, homogen und isotrop sein. Die Ausdehnung des Grundwasserleiters wird als unbegrenzt angenommen. Des weiteren weist der Grundwasserleiter eine konstante Mächtigkeit und eine horizontale Piezometerhöhe auf. Die Entnahmemenge aus dem Brunnen muss konstant sein und Speichereffekte des Brunnens werden vernachlässigt. Die zu lösende Gleichung lautet:

Als Anfangsbedingung wird h(0,r) = h0 für alle r gesetzt. Für die Randbedingungen gilt:

für t > 0

für alle t.
Daraus lässt sich die analytische Lösung ableiten zu:

darin bedeutet:



Damit erhält man:

In der Praxis findet die folgende Näherung Verwendung:

Hierbei wird ab einem Zeitpunkt t ein Fehler ε toleriert. Der Fehler beträgt bei:
@simon siehe https://staging.delta-h.de/lehre/veri/index.htm
muss immer in eine Zeile

ε < 5%

ε < 2%

ε < 1%
Somit ergibt sich der Funktionsverlauf für die Näherungslösung zu:

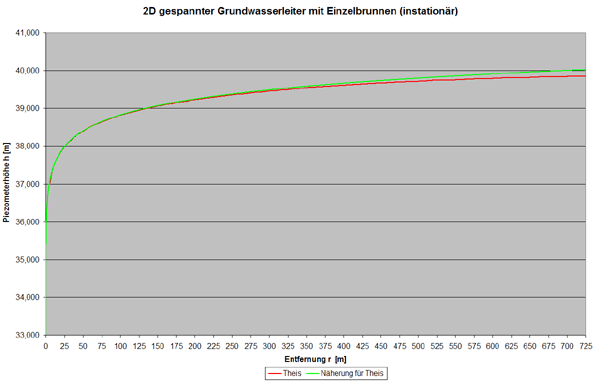
Eine Gegenüberstellung dieser zwei Ergebnisse zeigt, dass die maximale Abweichung in einer Entfernung von 725m zum Brunnen etwa 16 cm beträgt.
Diskretisierung
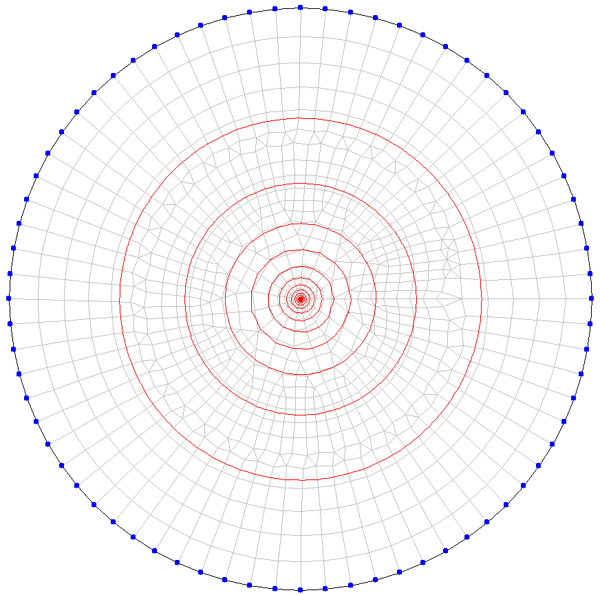
In der Brunnen_ge_is.zip Datei befindet sich die Datei Brunnen_gesp_instat.net. Mit dieser Netzdatei ist die Verifizierung durchgeführt worden. Es wurde ein Horizontalmodell mit der Zeiteinheit Jahr erstellt. Die Eingabeparameter stehen in der Tabelle im Abschnitt "Modell und Parameter". Das verwendete Netz ist in der folgenden Abbildung dargestellt.
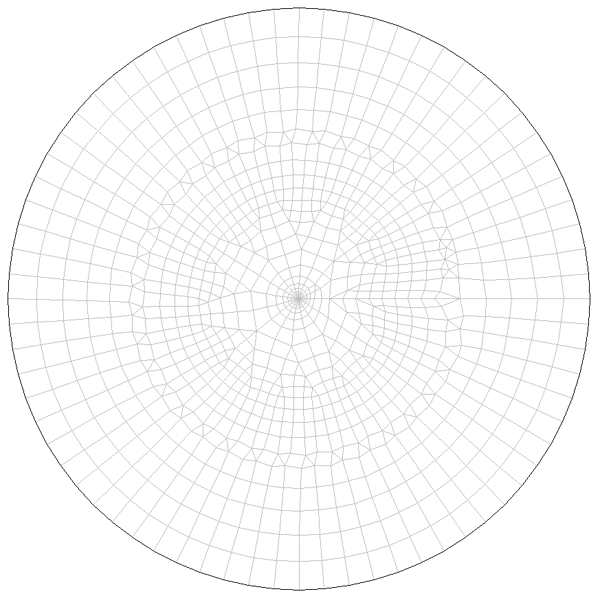
Vergleich der Berechnungsergebnisse
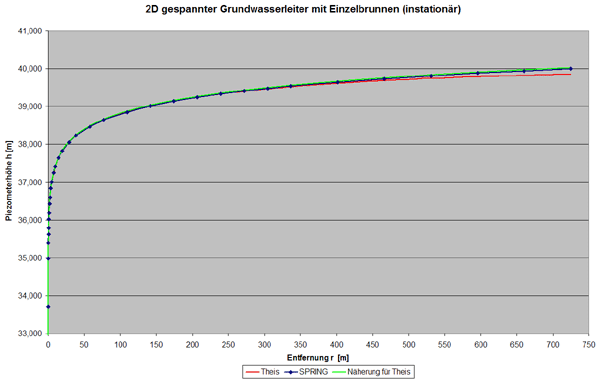
In der folgenden Abbildung sind die Ergebnisse von SPRING und der analytischen Lösung gegenüber gestellt. Die analytische Lösung ist mit der Datei Brunnen_gesp_instat.xls berechnet worden. Diese befindet sich ebenfalls in der brunnen_ge_is.zip Datei. Es ist deutlich zu sehen, dass die Lösung von SPRING kaum abweicht.
Literatur
[David] Ioan David; Grundwasserhydraulik Strömungs- und Transportvorgänge, Vieweg, 1997
[Kinzelbach] W. Kinzelbach; Numerische Methoden zur Modellierung des Transports von Schadstoffen im Grundwasser, Oldenbourg, 1987
[Kinzelbach] W. Kinzelbach und Rausch, R., Grundwassermodellierung Eine Einführung mit Übungen, Gebrüder Bornträger, 1995
[SPRING] SPRING; Simulation of Processes in Groundwater, Programm- beschreibung,Version 3.2